已知:如下图,A、B两点是直线l同旁的两个定点问题:在直线l上求一点P,使得PA+PB的值最小.
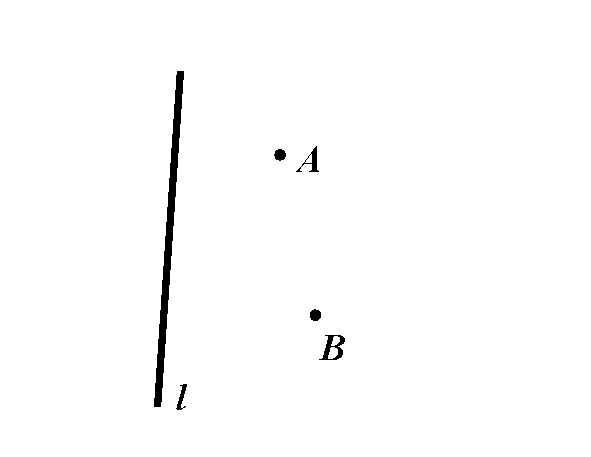
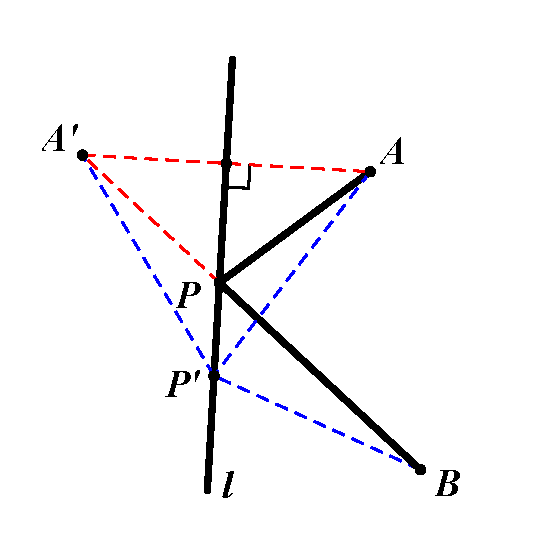
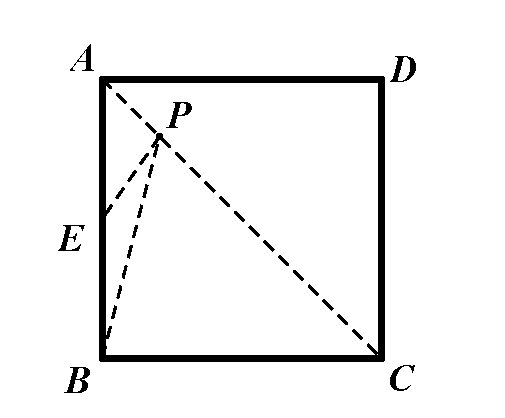
剖析:作点A关于直线l的对称点A,连结AB,交直线于点P,此时PA+PB=AB最小.证明过程非常简单,在直线上再任取一点P,PA=PA,PA+PB=PA+PB>AB,所以点P是所求.模型应用:(1)如图,正方形ABCD边长为2,点E是边AB中点,点P是对角线AC上一点.则PE+PB的最小值是 .
(2)如图,⊙O的半径为2,点A、B、C在⊙O上,OAOB,AOC=60,P是OB上一点,则PA+PC的最小值是.
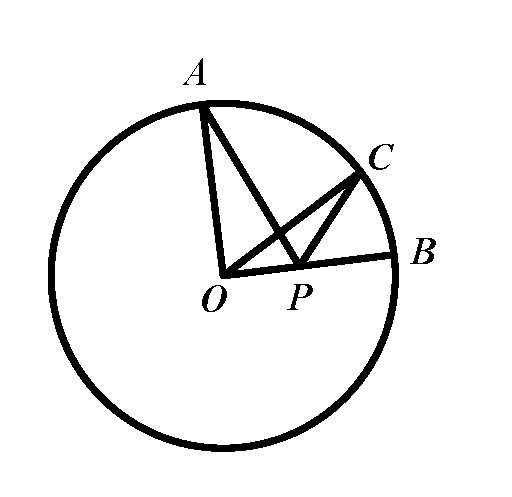
(3)如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,4),点C、D分别是OA、AB的中点,P是OB上一点,求△PCD周长的最小值.
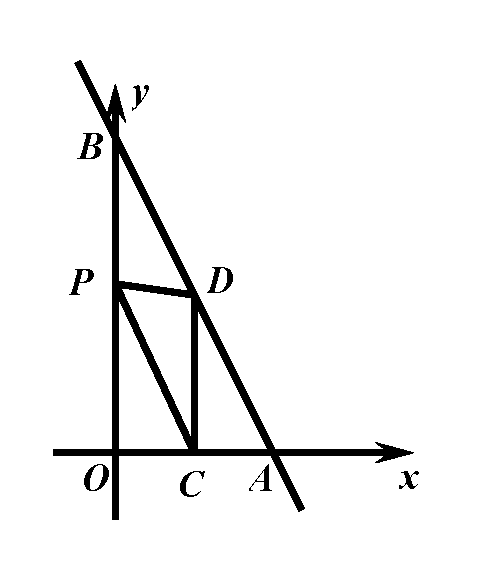
以上几题是模型1在不同题型中的运用,同学们假如能练成火眼金睛,擅长在变化的条件中找到不变的数学模型,以不变应万变,就能像孙奥创一样成为考场上的斗战胜佛.假如把模型1中的条件稍作调整,又可以得到它的一些推广模型.答案:

推广1:已知:如图,点P是AOB内肯定点.问题:分别在OA、OB边上找点M、N,使△PMN的周长最小.
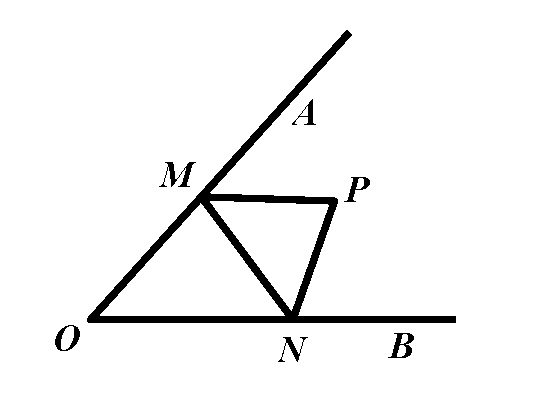
剖析:△PMN的周长=PM+MN+NP,可以借助作轴对称,把这三条线段转化为同一直线上的线段.如图,分别作点P关于OA、OB的对称点P、P,连结PP,分别交OA、OB于点M、N,连结PM、PN,此时PM=PM,PN=PN,△PMN的周长=PM+MN+NP=PP,此时周长最小.
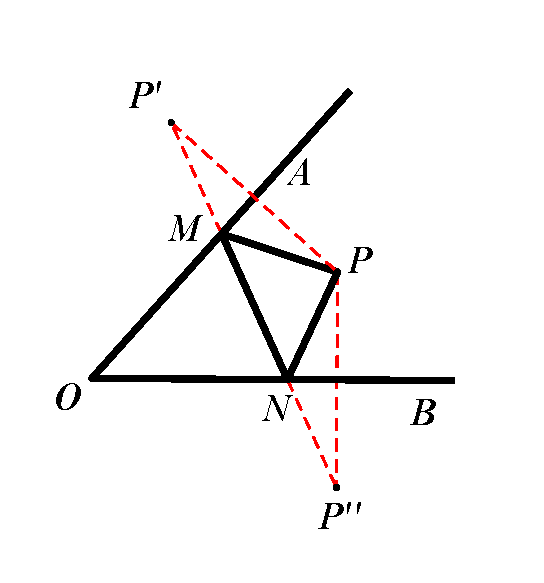
模型应用:如图,点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,则△CDE周长的最小值是

.答案:
10推广2:已知:点P、Q是AOB内部两定点.问题:分别在直线OA、OB上找点M、N,使四边形PMNQ的周长最小.
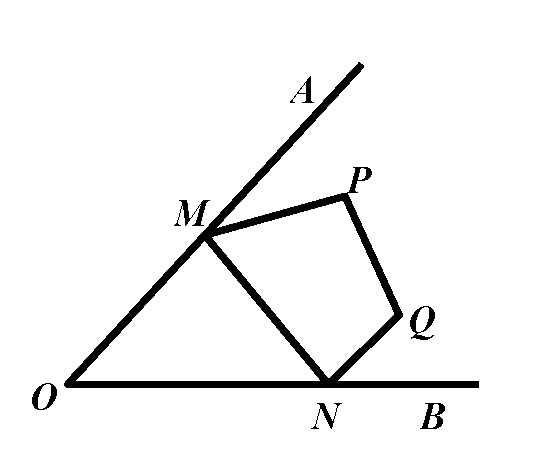
剖析:由于PQ的长度是定值,要使四边形PMNQ的周长最小,就是要使PM+MN+NQ的值最小.作点P关于OA的对称点P,作点Q关于OB的对称点Q,连结PQ,分别交直线OA、OB于点M、N,连结PM、MN、NQ,由于PM=PM,QN=QN,所以四边形PMNQ的周长=PM+MN+NQ+QP=PQ+PQ,由于PQ是定值,而PM+MN+NQ的最小值为PQ的长度,所以此时四边形PMNQ的周长最小.
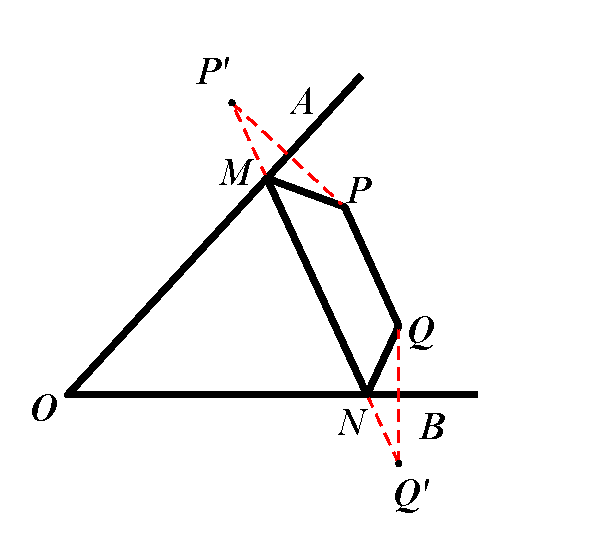
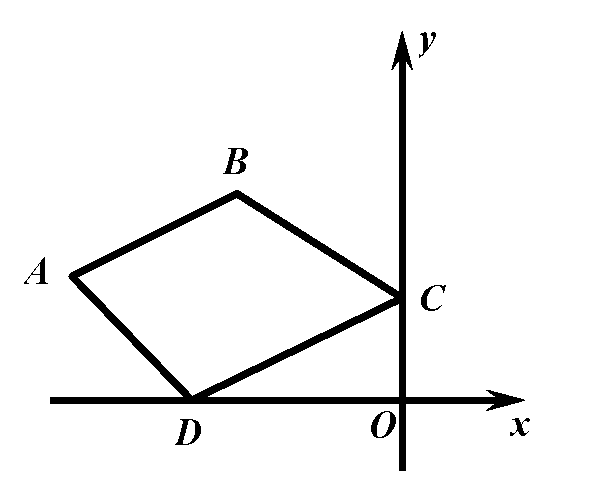
模型应用:在平面直角坐标系中,点A(-8,3),点B(-4,5),点C(0,n),点D(m,0),当四边形ABCD周长最短时,求m:n的值.
答案:
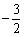
在变化万千的已知条件下,可以找到不变的规律,这与《易经》中讲解的变与不变的智慧相吻合.人类最高的智慧,就是以不变应万变,这也是数学学习的无敌秘籍.